Selection Sort

Selection sort: select the minimum value!

• Selection sort Algorithm
  • Finds minimum value in given data
  • Replace this minimum with the value at the beginning of the data
  • Repeat the rest of the data in the same way except for the first one

Code Design

sorted from the begining of the data
Every each time the for loop executes, sort after the first index value from the previous loop
turn : One rotation turn of condition check for all list

1. two datas for selection sort
   (3 2)
   (2 3)

   data index for comparing	comparing start point index	comparing end point index
   0	1	1

2. three datas for selection sort
   (3 4 2)
   (2 4 3)
   (2 3 4)

   data index for comparing	comparing start point index	comparing end point index
   0	1	2
   1	2	2

3. four datas for selection sort
   (4 5 3 2)
   (2 5 3 4)
   (2 3 5 4)
   (2 3 4 5)

   data index for comparing	comparing start point index	comparing end point index
   0	1	3
   1	2	3
   2	3	3

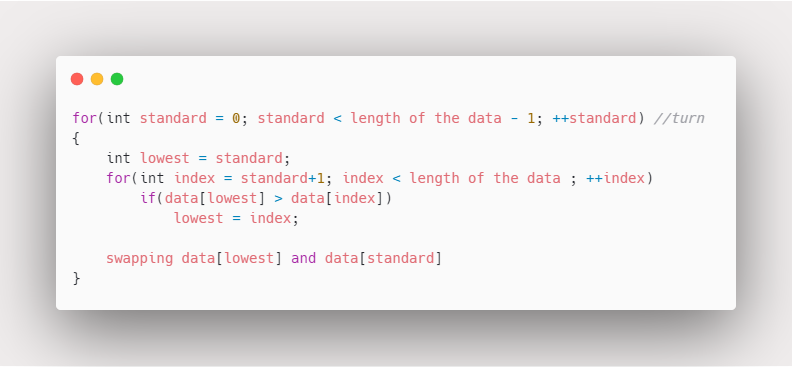
Pseudocode

1. for(int standard = 0; standard < len(data_list) - 1 ; ++standard) : repeat for loop
2. lowest = standard
3. for(int index = 0; index < len(data_list); ++index) : repeat after standard
   • if( data_list[lowest] > data_list[index] )
     • lowest = index
4. swapping two data
   • data_list[index] <=> data_list[lowest]

Time Complexity

two for loops : $O(n^2)$

C++ code implementation

#include<iostream>
using namespace std;

void selectionSort(int * data, int size)
{
	for(int standard = 0; standard < size-1 ; ++standard)  //turn 
	{
		int lowest = standard;
		for(int index = standard+1; index < size; ++index)
		{
			if(data[lowest] > data[index])
				lowest = index;
		}
		int temp = data[lowest];
		data[lowest] = data[standard];
		data[standard] = temp;
	}
}
int main()
{
	int list_s[] = {4,5,3,2,1};
	
	int len = sizeof(list_s) / sizeof(list_s[0]);
	cout  << len << endl;
	
	for(int i = 0; i < len; ++i)
		cout << list_s[i] << endl;
		
	selectionSort(list_s, len);
	
	for(int i = 0; i < len; ++i)
		cout << list_s[i] << endl;
		
		
	return 0;
	
}

Bubble sort

Bubble sort: repeatedly steps through the list, compares two adjacent datas and swaps them if they are in the wrong order

Code Design

• condition check : Compare two datas
• turn : One rotation turn of condition check for all list

1. two datas for bubble sort
   (3 2)
   (2 3)
   condition check : 1
turn : 1

2. tree datas for bubble sort
   (5 4 3)
   (4 3 5)
   (3 4 5)
   condition check : 2
turn : 2

3. four datas for bubble sort
   (5 4 3 2)
   (4 3 2 5)
   (3 2 4 5)
   (2 3 4 5)
   condition check : 3
turn : 3

Pseudocode

• length of the entire data - i -1
• The reason for - i
  • the bubble sort will be executed only on unsorted data
  • last index of the list will be sorted every each turn
  • therfore, reduce the number of repetitions (reduce the count of the loop)

1. for num in range(len(data_list)) : repeat
2. swap = false (make a flag to check swap was executed)
3. Inside the second roop, for index in range(len(data_list) - i - 1) : repeat
4. If data_list[index] > data_list[index + 1]
   • Swapping two datas
   • swap = true
5. If swap == false : break, because the list is already sorted

Time Complexity

two for loops : $O(n^2)$

If entire lists are already sorted, the time complexity is O(n)

C++ code implementation

#include<iostream>
using namespace std;

void bubbleSort(int * data, int size)
{
	for(int i = 0; i < size-1 ; ++i)
	{
		bool swaps = false;
		for(int index = 0; index < size - i - 1; ++index)
		{
			if(data[index] > data[index+1])
			{
				int temp = data[index];
				data[index] = data[index+1];
				data[index+1] = temp;
			}
			swaps = true;
		}
		if(!swaps)
			break;
	}
}
int main()
{
	int list_b[] = {5,4,3,2,1};
	
	int len = sizeof(list_b) / sizeof(list_b[0]);
	cout  << len << endl;
	
	for(int i = 0; i < len; ++i)
		cout << list_b[i] << endl;
		
	bubbleSort(list_b, len);
	
	for(int i = 0; i < len; ++i)
		cout << list_b[i] << endl;
		
		
	return 0;
	
}

힙(Heap)

힙: 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)
완전 이진 트리: 노드를 삽입 할 때 최하단 왼쪽 노드부터 차례대로 삽입하는 트리
힙 (자료구조)

• 힙을 사용하는 이유
  • 배열에 데이터를 넣고, 최대값과 최소값을 찾으려면 O(n)이 걸림
  • 이에 반해 힙에 데이터를 넣고, 최대값과 최소값을 찾으면 O(log n)이 걸림
  • 힙 - 최대값 또는 최소값을 빠르게 찾아야하는 자료구조 및 알고리즘 구현에 활용

힙 구조

1. 완전 이진 트리 형태를 가짐
2. 각 노드의 값은 해당 노드의 자식노드의 가진 값과 관련된 조건이 있음
   • 최대힙 (Max-Heap)
     • 최대 값을 구하기 위한 구조
     • 각 노드의 값은 해당 노드의 자식 노드가 가진 값보다 크거나 같음
   • 최소힙 (Min-Heap)
     • 최소 값을 구하기 위한 구조
     • 각 노드의 값은 해당 노드의 자식노드가 가진 값보다 작거나 같음

힙과 이진 탐색 트리

힙은 최대/최소 검색을 위한 구조
이진 탐색 트리는 탐색을 위한 구조

• 공통점
  • 힙과 이진 탐색트리는 모두 이진 트리
• 차이점
  • 힙은 각 노드의 값이 자식 노드보다 크거나 같음 (Max-Heap의 경우)
  • 이진 탐색 트리는 왼쪽 자식 노드의 값이 가장 작고, 그다음 부모 노드, 그 다음 오른 쪽 자식 노드 값이 가장 큼
  • 힙은 이진 탐색 트리의 조건인 자식 노드에서 작은 값은 왼쪽, 큰 값은 오른쪽 이라는 조건이 없음

힙 시간 복잡도

• O(log n)
  • n개의 노드를 가지는 힙에 데이터 삽입, 또는 삭제시, 최악의 경우 root노드에서 leaf노드까지 비교해야하므로 트리의 높이 depth = log n 에 가까움
  • log의 밑은 2
  • 한번 실행시마다 50%의 실행시간을 단축

힙 동작

1. 힙에 데이터 삽입
   • 힙은 완전 이진 트리이므로, 삽입할 노드는 최하단 부 노드부터 채워짐
   • 데이터 삽입 이후, 부모 노드보다 값이 클 경우 부모노드와 위치를 바꿔주는 swap 작업 반복
2. 힙에 데이터 삭제
   • 보통 root노드(최상단 노드)를 삭제하게됨
     • 힙의 용도는 최대 값 또는 최소 값을 root노드에 놓아서 최대값과 최소값을 바로 꺼내서 쓸 수 있도록 하는 것
   • 상단의 root 노드 데이터 삭제시, 가장 최하단 부 왼쪽노드(가장 마지막에 추가한 노드)를 root노드로 이동
   • root노드 값이 child node보다 작을 경우, child node중 가장 큰 값을 가진 노드와 root 노드 위치를 바꿔줌 (swap)

힙 구현

• 일반적으로 힙 구현시 배열자료구조를 활용
• 배열은 인덱스가 0부터 시작하지만, 구현의 편의를 위해 root노드의 인덱스 번호를 1로 지정
  • 부모 노드 인덱스 번호 (parent node's index) = 자식 노드 인덱스 번호 (child node’s index) / 2
  • 왼쪽 자식 노드 인덱스 번호 (left child node's index) = 부모 노드 인덱스 번호 (parent node’s index) * 2
  • 오른쪽 자식 노드 인덱스 번호 (right child node's index) = 부모 노드 인덱스 번호 (parent node’s index) * 2 + 1

C++ code

C++의 경우 std namespace에 정의된 heap 표준 문법이 있음
algorithm 헤더 파일에 정의
C++ Heap - Std namespace에 정의된 heap 표준문법

• 힙 구현 std::make_heap
• 힙 데이터 삽입 std::push_heap
• 힙 데이터 삭제 std::pop_heap
• std::is_heap

#include <iostream>
#include <algorithm>
#include <functional>
#include <vector>
using namespace std;

int main()
{
    vector<int> v { 3, 2, 4, 1, 5, 9 };

    cout << "initially, v: ";
    for (auto i : v) 
		cout << i << ' ';
    cout << '\n';

	if (!std::is_heap(v.begin(), v.end())) {
        cout << "making heap...\n";
        make_heap(v.begin(), v.end());
    }
    cout << "after make_heap, v: ";
    for (auto i : v) 
		cout << i << ' ';
    cout << '\n';
 
	v.push_back(6);
	push_heap(v.begin(), v.end());
	
	cout << "after push_heap: ";
    for (auto i : v) 
		cout << i << ' ';
    cout << '\n';

    pop_heap(v.begin(), v.end());
 
    cout << "after pop_heap, v: ";
    for (auto i : v) 
		cout << i << ' ';
    cout << '\n';
 
    auto top = v.back();
    v.pop_back();
    cout << "former top element: " << top << '\n';
 
    cout << "after removing the former top element, v: ";
    for (auto i : v) 
		cout << i << ' ';
    cout << '\n' << '\n';
 
    return 0;
}