Algorithm - DFS (Concept, Time Complexity and C++)
DFS (Depth First Search)
- Main graph Search algorithm
BFS (Breadth First Search): Search for brother nodes at the same level of the vertex first
DFS (Depth First Search): search for the children of vertex first
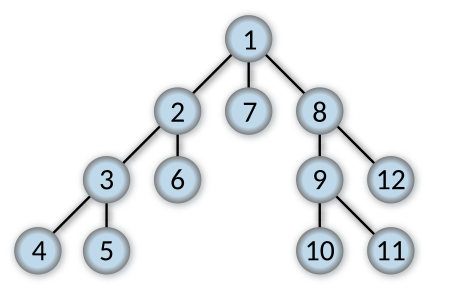
DFS Algorithm
- Utilize Queue and Stack
- Note that the BFS data structure uses two queues, while DFS uses a stack and a queue.
Time Complexity
- DFS Time Complexity
- Number of Vertexes: V
- Number of Edges: E
- Time Complexity: O(V + E)
C++
#include <iostream>
#include <cstdio>
#include <vector>
using namespace std;
int visited[13];
vector<int> graph[13];
void dfs(int start)
{
if(visited[start])
return;
visited[start] = true;
cout << start << " ";
for(int i = 0; i < graph[start].size(); ++i)
{
int next_index = graph[start][i];
dfs(next_index);
}
}
int main()
{
graph[1].push_back(2);
graph[2].push_back(1);
graph[2].push_back(3);
graph[3].push_back(2);
graph[3].push_back(4);
graph[4].push_back(3);
graph[3].push_back(5);
graph[5].push_back(3);
graph[2].push_back(6);
graph[6].push_back(2);
graph[1].push_back(7);
graph[7].push_back(1);
graph[1].push_back(8);
graph[8].push_back(1);
graph[8].push_back(9);
graph[9].push_back(8);
graph[9].push_back(10);
graph[10].push_back(9);
graph[9].push_back(11);
graph[11].push_back(9);
graph[8].push_back(12);
graph[12].push_back(8);
dfs(1);
return 0;
}
- Recursive call works as Stack
