Algorithm - (11) DFS

DFS (Depth-First Search)

• 대표적인 그래프 탐색 알고리즘
  • 너비 우선 탐색 (Breadth First Search): 정점들과 같은 레벨에 있는 노드들 (형제 노드들)을 먼저 탐색하는 방식
  • 깊이 우선 탐색 (Depth First Search): 정점의 자식들을 먼저 탐색하는 방식

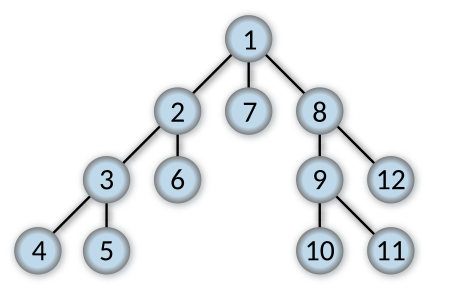
DFS 알고리즘 구현

• 자료구조 스택과 큐를 활용함
  • need_visit !!스택!!과 visited 큐, 두 개의 자료 구조를 생성
    ​

    BFS 자료구조는 두 개의 큐를 활용하는데 반해, DFS 는 스택과 큐를 활용한다는 차이가 있음을 인지해야 함

DFS 시간 복잡도

• 일반적인 DFS 시간 복잡도
  • 노드 수: V
  • 간선 수: E
  • 시간 복잡도: O(V + E)

C++

#include <iostream>
#include <cstdio> 
#include <vector>

using namespace std;

int visited[13];
vector<int> graph[13];
 
void dfs(int start)
{
	if(visited[start])
		return;
	visited[start] = true;
	cout << start << " ";
	
	for(int i = 0; i < graph[start].size(); ++i)
	{
		int next_index = graph[start][i];
		dfs(next_index);
	}
}

int main()
{
	graph[1].push_back(2);
	graph[2].push_back(1);
	
	graph[2].push_back(3);
	graph[3].push_back(2);
	
	graph[3].push_back(4);
	graph[4].push_back(3);
	
	graph[3].push_back(5);
	graph[5].push_back(3);

	graph[2].push_back(6);
	graph[6].push_back(2);
	
	graph[1].push_back(7);
	graph[7].push_back(1);
	
	graph[1].push_back(8);
	graph[8].push_back(1);
	
	graph[8].push_back(9);
	graph[9].push_back(8);

	graph[9].push_back(10);
	graph[10].push_back(9);	
		
	graph[9].push_back(11);
	graph[11].push_back(9);
	
	graph[8].push_back(12);
	graph[12].push_back(8);
	
	dfs(1);
	
	return 0;
}

• 재귀함수는 _스택_처럼 동작
• 보통 프로그래밍 문제를 풀이할 때 stack 을 구현하기보다는 재귀함수를 호출하면 더 코드가 깔끔

Python

• 파이썬에서 제공하는 딕셔너리와 리스트 자료 구조를 활용해서 그래프를 표현할 수 있음

graph = dict()

graph['A'] = ['B', 'C']
graph['B'] = ['A', 'D']
graph['C'] = ['A', 'G', 'H', 'I']
graph['D'] = ['B', 'E', 'F']
graph['E'] = ['D']
graph['F'] = ['D']
graph['G'] = ['C']
graph['H'] = ['C']
graph['I'] = ['C', 'J']
graph['J'] = ['I']

​

def dfs(graph, start_node):
    visited, need_visit = list(), list()
    need_visit.append(start_node)
    
    while need_visit:
        node = need_visit.pop()  #맨 끝데이터 
        if node not in visited:
            visited.append(node)
            need_visit.extend(graph[node])
    
    return visited

Direct Link